Unlocking the Mysteries of Brownian Motion: From Chaos to Clarity
Written on
The Enigmatic Nature of Brownian Motion
Brownian motion, named after the botanist Robert Brown, represents a captivating phenomenon where particles suspended in a fluid exhibit random movement due to interactions with fluid molecules. Picture observing pollen grains in water under a microscope, dancing unpredictably without any clear cause. This seemingly erratic behavior is, in fact, a well-documented and predictable occurrence in physics and mathematics. Rather than being a mere random trajectory, Brownian motion reveals the fundamental structure of randomness itself. Gaining insight into this motion aids scientists and engineers in creating enhanced materials, predicting market trends, and even deciphering biological mechanisms at a molecular scale.
The Geometry of Random Trajectories
When discussing the convex hull of Brownian motion, we refer to the smallest convex shape that can contain the entire trajectory of a particle. This concept becomes increasingly fascinating as we consider higher dimensions. Envision a particle navigating through a 3D space, and then extend this thought to four, five, or even more dimensions. Geometric metrics such as volume, surface area, diameter, and circumradius of these convex hulls provide valuable insights into the characteristics of high-dimensional spaces. Understanding these metrics is vital for comprehending how these shapes evolve, their limits, and their overall configuration, with implications spanning fields from data science to quantum physics.
To further illustrate the dynamics of geometric functionals in Brownian motion, we can visualize the expected trends of volume, surface area, diameter, and circumradius over time.
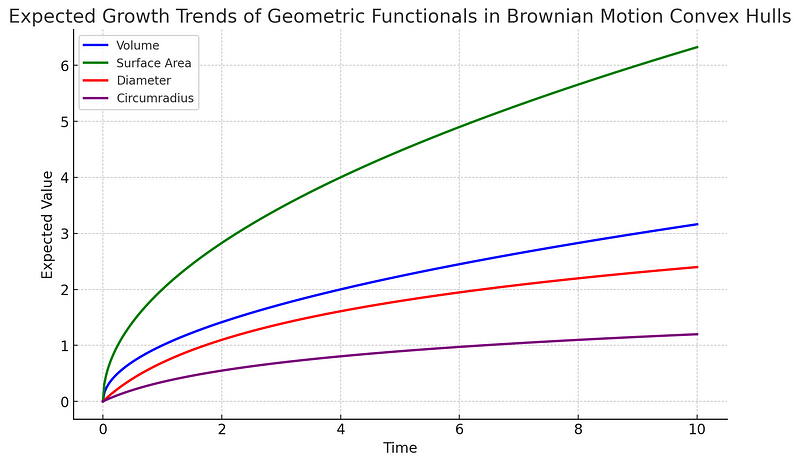
A Measure of Growth
Inverse processes allow us to determine the duration required for a geometric functional, such as volume or surface area, to surpass a specific value. This is akin to asking, “How long will it take for the convex hull to expand enough to cover a designated area?” Such processes are essential in disciplines that depend on temporal measurements and forecasts. For example, in finance, this could relate to the time needed for an asset’s price to achieve a certain threshold. In physics, it aids in understanding diffusion phenomena. Investigating these processes in higher dimensions broadens our comprehension from the familiar three-dimensional realm to the more abstract and fundamentally significant higher-dimensional spaces.
The Importance of This Research
The study of Brownian motion and its convex hulls in higher dimensions transcends mere theoretical exploration. It bears practical implications across numerous domains. For instance, in computer science, algorithms that handle extensive datasets often operate within high-dimensional contexts. Grasping the behavior of Brownian paths can enhance these algorithms, leading to more efficient data processing. In physics and chemistry, this knowledge contributes to the analysis of molecular behavior and the creation of innovative materials. Even in our daily technology, from smartphones to AI systems, the principles derived from this research significantly enhance performance and functionality.
The Universal Scaling Principle
Brownian motion adheres to a universal scaling law, indicating that the length of the path increases in proportion to the square root of time. This foundational principle is instrumental in modeling various natural occurrences, from the diffusion of particles in liquids to fluctuations in stock prices.
Fractal Characteristics of Paths
The paths traced by Brownian particles exhibit fractal-like properties, implying they are self-similar at different scales. This characteristic establishes Brownian motion as a foundational aspect in the study of fractals and chaos theory, influencing fields such as meteorology and geology.
Einstein’s Contributions
Albert Einstein’s groundbreaking 1905 paper on Brownian motion provided critical evidence for the existence of atoms and molecules. His research laid the foundation for modern statistical mechanics and thermodynamics, revolutionizing our understanding of matter.
Medical Applications
Comprehending Brownian motion is vital in medicine, particularly concerning drug delivery systems. Nanoparticles engineered to traverse the bloodstream utilize the principles of Brownian motion to target specific areas within the body, thereby enhancing treatment effectiveness.
Financial Market Models
Models based on Brownian motion are widely utilized in finance for predicting stock prices and market movements. The random walk theory, grounded in Brownian principles, posits that short-term stock price fluctuations are inherently unpredictable, influencing investment strategies globally.
A Future Full of Opportunities
The investigation of Brownian motion and its geometric attributes in higher dimensions paves the way for new technologies and scientific advancements. By delving into the complexities of random paths, we can create more robust algorithms, design superior materials, and even refine medical treatments. The research extends beyond theoretical physics or pure mathematics; it influences various facets of our lives, subtly improving the technology we rely on and the scientific principles we trust. This ongoing exploration into the realm of randomness promises not only new knowledge but also innovative ways to leverage that knowledge for societal benefit.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your crystal ball into the future of technology. ? Subscribe for new insight videos every Saturday!
Watch us on YouTube