Exploring the P vs NP Dilemma: A Deep Dive into Computational Theory
Written on
Understanding the P vs NP Problem
The P vs NP problem stands as one of the most significant unresolved issues in the realm of computer science, and arguably in mathematics as a whole. Beyond the allure of the million-dollar prize, the assumption that P does not equal NP is foundational to virtually all online security measures, including those used for credit card transactions and Bitcoin mining. A proof that P equals NP would fundamentally alter our comprehension of computation and problem-solving methodologies.
To clarify, P denotes the set of problems that can be solved in polynomial time, while NP encompasses those that can be verified in polynomial time.
Polynomial functions, as you might recall from algebra, are expressions where all the exponents are positive integers. For instance, f(x) = 4x² + 7x³ - x + 1.5 is a polynomial.
The Travelling Salesman Problem serves as a prime example of an NP problem. The challenge lies in discovering a route that visits every city on a map while adhering to a specified distance limit (e.g., a total travel distance of less than 200 km).
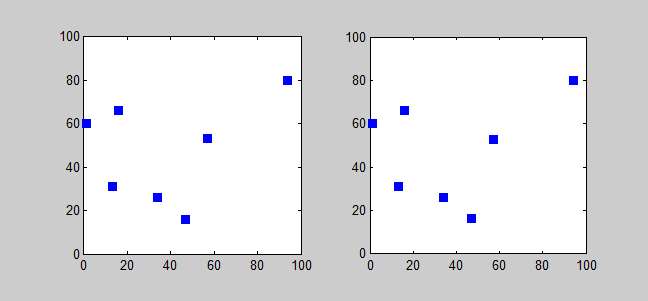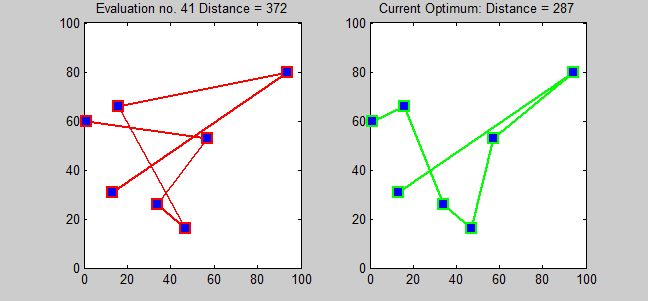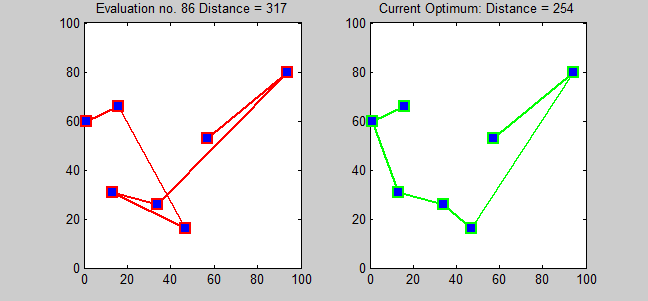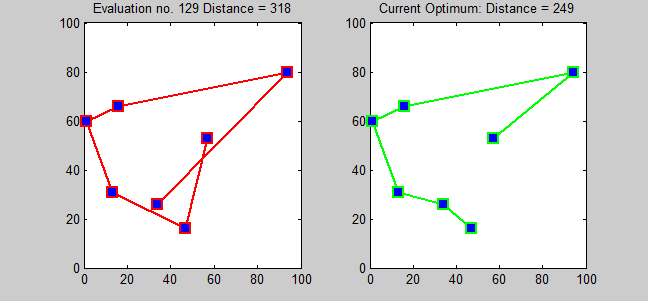
As the number of cities (n) increases, the possible routes increase exponentially, with (n - 1)!/2 potential routes. For 100 cities, this amounts to around 10²⁵ routes to evaluate. The rapid nature of exponential growth is astounding! While there are more efficient approaches than brute force, no known polynomial-time algorithm exists to solve this particular problem.
However, if you were to provide a specific route, I could verify whether it falls within the 200 km limit by simply summing the distances and responding with 'yes' or 'no'. This ability to confirm a solution in polynomial time indicates that the Travelling Salesman Problem belongs to the NP category.
If P were to equal NP, it would mean that every problem verifiable in polynomial time could also be solved in polynomial time. In such a world, a polynomial-time algorithm would exist for the Travelling Salesman Problem, as well as for other NP problems like the subset-sum problem, graph-clique problem, and the RSA algorithm used in credit card encryption and elliptic curve cryptography for Bitcoin.
So, what does the 'N' in NP signify?
The Meaning Behind 'N': Non-Deterministic Computation
The 'N' stands for 'non-deterministic'. NP problems are defined as those that can be solved in polynomial time by a non-deterministic Turing machine, and this definition has been validated to be equivalent to the verification definition.
Wikipedia succinctly explains, “NP is the set of decision problems for which the instances with a 'yes' answer have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively, the set of problems that can be solved in polynomial time by a non-deterministic Turing machine.”
You may wonder about the concept of a non-deterministic Turing machine.
A Turing machine is a theoretical model of computation that follows a set of instructions (an algorithm) to write symbols on a 'tape', allowing it to solve a wide array of computational problems. A non-deterministic Turing machine, however, is an even more abstract concept, capable of transitioning into multiple states simultaneously. Its non-deterministic nature means that the next state isn’t solely dictated by the previous one.
This phrase, 'even more theoretical', is used because while traditional Turing machines serve as a reasonable model for how computers operate (despite their infinite memory), non-deterministic Turing machines remain purely hypothetical. We currently lack computers that can function across multiple parallel realities and return with results from their exploration!
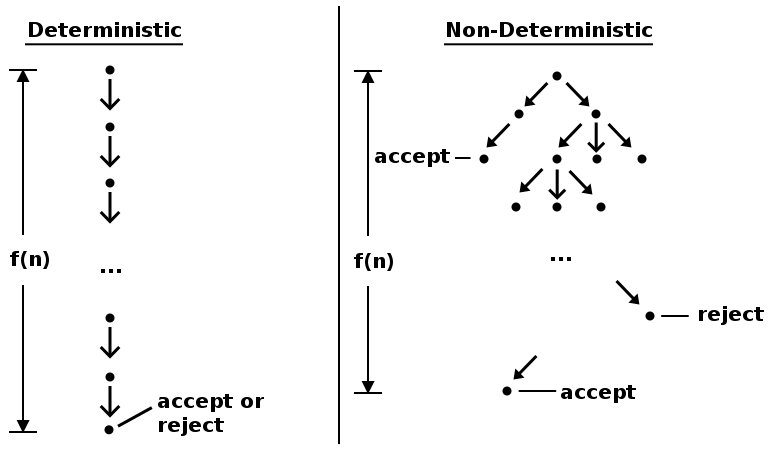
The Historical Context of Non-Deterministic Machines
The notion of nondeterminism in computation was introduced by Rabin and Scott in their 1959 paper, "Finite Automata and Their Decision Problems." They posited that a nondeterministic automaton is not probabilistic but rather a machine that can choose from several options in its operations. At any point in its process, it can select from multiple internal states. While some sequences of choices may lead to dead ends, we consider a tape acceptable if at least one sequence results in a designated final state.
Although Rabin and Scott suggested finite automata as an alternative to Turing machines, the nondeterminism concept gained traction while Turing machines remained the standard model. In 1971, Stephen Cook published "The Complexity of Theorem-Proving Procedures," which is now viewed as the inception of the P vs NP problem, framing it in terms of nondeterministic Turing machines.
Cook's first theorem stated that if a set S of strings is accepted by a nondeterministic Turing machine within polynomial time, then S is P-reducible to {DNF tautologies}. He also identified the first NP-complete problem: the Boolean Satisfiability Problem (SAT), which determines whether a given Boolean formula can be satisfied by some combination of its variables.
The recognition that Boolean Satisfiability is NP-complete is termed the Cook-Levin Theorem, which opened the doors for Richard Karp, who in 1972 identified 21 NP-complete problems, including the Graph Clique and Hamiltonian Cycle problems (also known as the Travelling Salesman Problem). Today, there are thousands of established NP-complete problems.
Exploring the P vs NP Question
A question that often arises is: Why define NP in terms of nondeterministic Turing machines rather than using the more intuitive perspective of problems verifiable in polynomial time?

One possible explanation lies in these two related facts: the nondeterministic Turing machine framework allows for a unified approach to both P and NP. We face a problem with an unknown solution and must ask, “What would be necessary to resolve it?” Conversely, the verification definition requires us to start with a solution.
The mathematical structure of a nondeterministic Turing machine is quite similar to that of a traditional deterministic Turing machine. The only significant change is that rather than transitioning from one state to the next, we establish a relation to all potential states. This similarity is mathematically convenient for comparing problems within P and NP.
However, the verification definition may be more beneficial for the vast majority of individuals seeking a conceptual grasp of the P vs NP dilemma. Importantly, it has been established that both definitions are mathematically equivalent.
So, should we frame the problem as P vs VP instead?
I would argue yes! Yet, I acknowledge that I am not an expert in this domain. If you have insights on this topic, feel free to share your thoughts in the comments.
The first video, "The N-Word 'Double Standard'," delves into the complexities of societal perceptions and the implications of language.
The second video, "Bill Burr: How You Know the N Word is Coming," offers a comedic take on expectations and societal norms in language usage.