Section 1.1: Geometry of Functions

We are all familiar with the basics of geometry, and our goal is to extend these intuitive ideas into a new mathematical environment.

Let's start by considering two-dimensional space. A point in this space can be easily understood and represented by its x-component and y-component, as illustrated below:

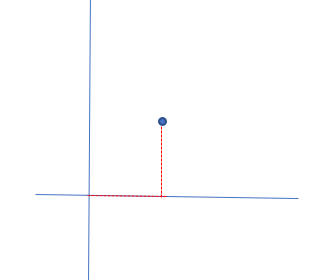
Similarly, we can extend this concept into three dimensions, where a point can be described by its height, width, and length. In two dimensions, we refer to the ‘x-axis’ and ‘y-axis,’ while in three dimensions, we add a ‘z-axis.’ The crucial aspect here is that these axes are perpendicular to each other, which is a broad idea that can be applied in various contexts.

Understanding mathematical objects as sums of simpler components is beneficial. For instance, by breaking down a point in two-dimensional space into its x and y components, we can visualize and manipulate it more effectively. Thus, a more generalized idea emerges: we should seek a subset of mathematical objects that can help construct others. We refer to this subset as a basis, which should ideally point in different directions, much like the perpendicularity of the axes.

Section 1.2: The Role of Trigonometric Functions

Now, let’s introduce two fundamental functions that will play a crucial role in our exploration: sin(x) and cos(x). These simple functions are remarkably versatile and can express a wide variety of other functions through clever mathematical techniques.

To visualize these functions, let’s consider how they relate to a circle of radius 1. When given an angle θ, the corresponding point on the circle can be expressed in terms of its x-direction (cos(θ)) and y-direction (sin(θ)).

While angles are often measured in degrees, mathematicians typically use radians, where a full circle corresponds to 2π radians. This choice simplifies many mathematical expressions, much like how different countries use various measurement systems for the same concepts.

Perpendicular Functions

A function is defined as a relationship that takes an input and returns an output. The graph of sin(x) below illustrates its periodic nature:

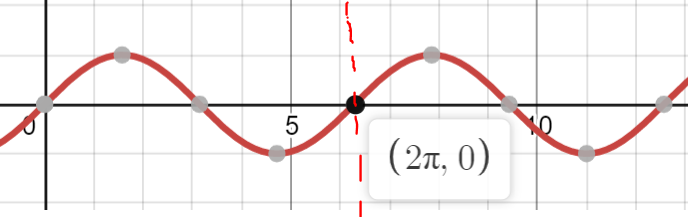
Suppose we have a function that exhibits regular periodic behavior and appears smooth enough to be drawn by hand.

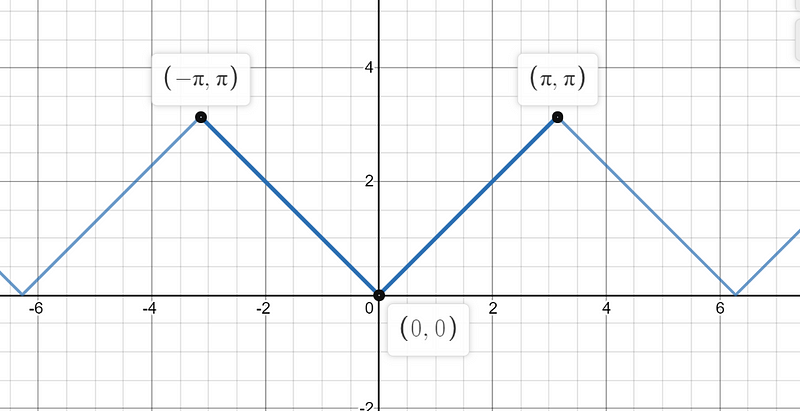
We can assert that such functions, which are both periodic and sufficiently smooth, can be represented as an infinite sum of trigonometric functions. The underlying principle is that these trigonometric functions exhibit a form of perpendicularity. It is fascinating how functions designed to aid in understanding circles possess such remarkable adaptability.

A Word of Caution

While many properties of familiar two- and three-dimensional spaces carry over to function spaces, some do not. For example, while only two perpendicular directions suffice to express any point in two-dimensional space, function spaces require a countably infinite number of perpendicular directions! This complexity adds depth to our exploration.

For those interested, the next section discusses the conditions of smoothness that mathematicians consider crucial for analysis.

Section 1.3: Exploring Orthogonality

The following segment may prove challenging. If you find yourself stuck, feel free to skip ahead to the next section, which applies the theory to our quest for the Basel Problem. However, take a moment to engage with this material—great insights often take time to assimilate!

We define the following trigonometric functions:

• sin(x), sin(2x), sin(3x), ...
• cos(x), cos(2x), cos(3x), ...

To understand the concept of perpendicular functions, we utilize integrals, particularly for the interval (-π, π). Two functions f(x) and g(x) are considered perpendicular if the integral of their product over this interval equals zero.

Continuing our exploration, we’ll demonstrate that sin(nx) and cos(mx) are indeed perpendicular functions.

This first video delves into a brilliant solution to the Basel Problem, showcasing the connection between complex integrals and the sum of 1/n².

Now, let’s examine the relationship between various sine and cosine functions.

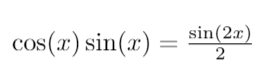
Through some algebraic manipulation, we can derive the following results:

1. For any integers n and m, sin(nx) is perpendicular to cos(mx).
2. For different integers n and m, sin(nx) is perpendicular to sin(mx), while cos(nx) is also perpendicular to sin(mx).
3. When n equals m, sin(nx) is not perpendicular to itself.

We summarize these findings as follows:

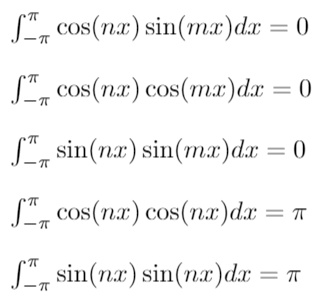
Once we confirm the orthogonality of our functions, we can express a function f(x) as an infinite sum of these trigonometric functions.

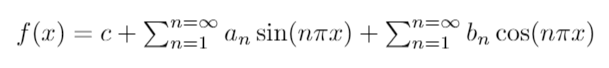
Now, let’s apply this knowledge to explore the Basel Problem further!

Appendix: Additional Insights on Fourier Series

For those interested in delving deeper, this section provides further details on the derivation and convergence of Fourier series, explaining some subtleties of the theory.

Let’s examine a worked example demonstrating how the orthogonality of functions can simplify our calculations.

As we progress through this material, we will gain a clearer understanding of why specific functions can represent others, particularly in the context of even and odd functions.

If you have made it this far, congratulations! I appreciate your interest, and I welcome your feedback on improving this article. Feel free to share your thoughts below!