How Prisms Separate Light into a Spectrum of Colors
Written on
Introduction to Light Phenomena
This fascinating physical occurrence is something we encounter regularly but often overlook. We witness it primarily in phenomena like rainbows, CDs, and prisms. The concept of dispersion is key to understanding how prisms refract light. Before delving into dispersion, let's first explore some fundamental properties of light. To clarify these concepts, I'll employ numerous analogies, as light can be quite an elusive subject in our universe—akin to a playful child.
Understanding Light
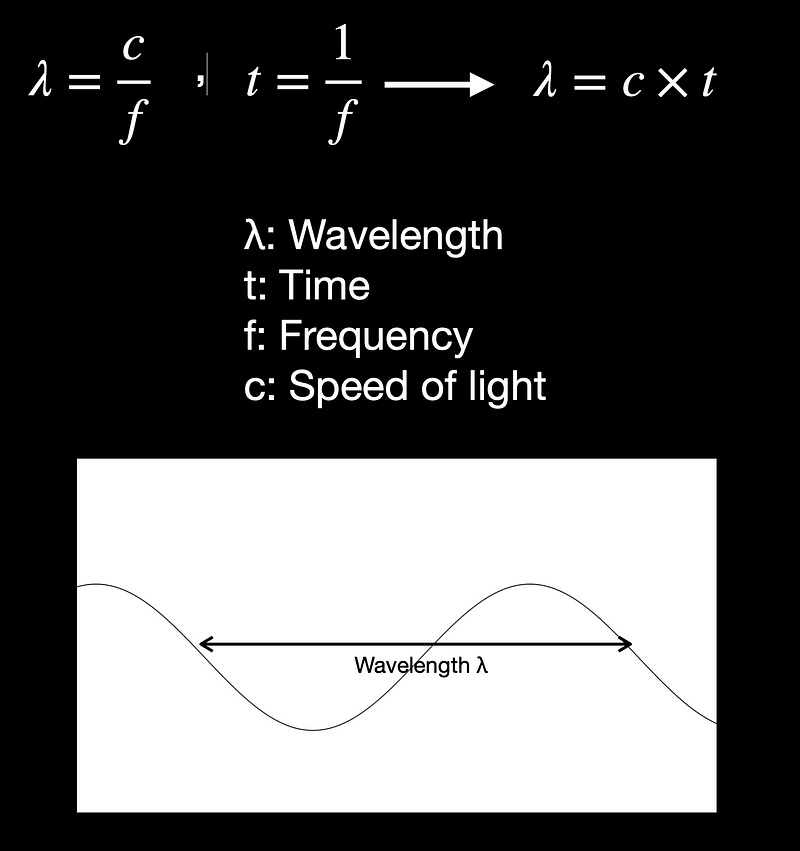
Light exhibits both wave-like and particle-like characteristics. Its speed in a vacuum is approximately ( c = 3 times 10^8 ) m/s. Recall Newton's equation for motion, where distance ( X = text{Velocity} times text{time} ). Similarly, the relationship between light's wavelength and frequency can be expressed as ( lambda = c times t ). These two concepts—wavelength and distance—are closely related, just as light speed ( c ) correlates with time (or the reciprocal of frequency).
However, this relationship holds true only in a vacuum. When light travels through a medium, its speed decreases. To quantify this, we introduce the refractive index, which indicates how much light slows down when interacting with different materials. This relationship can be expressed as ( n = frac{c}{v} ).

It's important to note that light doesn't actually slow down while in a medium; rather, it involves a cycle of absorption and emission. A helpful analogy compares a photon to a bus: each time it reaches a bus stop (an atom or molecule), it waits for passengers (energy) before continuing on its way. The rate of emission and absorption influences the refractive index.
How Prisms Create Color Spectrums
Now, let’s explore how a prism separates light into various color spectrums.

Dispersion Explained
Having established the necessary concepts about light, we can now understand how dispersion occurs. The wavelength of light is dependent on its frequency and the speed of light ( c ) can also be expressed as ( lambda = n times v times frac{1}{f} ). Rearranging gives us ( v = frac{lambda times f}{n} ). Since frequency remains constant, the speed of light in a medium is influenced solely by its wavelength. Consequently, red light, with a wavelength of about 633 nm, travels faster than purple light, which has a wavelength of around 380 nm. This difference in speed leads to the formation of a color spectrum.
To illustrate this, imagine an RC car on a carpet. When the car approaches the carpet at an angle, one wheel touches the carpet first, slowing it down compared to the other wheel that remains on the smoother surface. This differential in speed causes a change in the car's direction, similar to how light behaves as it enters a medium.

It’s crucial to remember that white light is a combination of various wavelengths. Since these wavelengths travel at different speeds, the angles at which they bend upon entering a medium differ. Referring back to our RC car analogy, if the car approaches the carpet at varying speeds, each speed results in a distinct angle. This phenomenon, known as dispersion, explains the visual effects we observe in prisms and rainbows. For instance, rainbows appear when light interacts with water droplets in the atmosphere, similar to how prisms function. The visibility of rainbows depends on factors such as the light's angle of incidence, the observer's location, and the density of water droplets in the air.
I hope this explanation clarifies the concept for you. Should you have any questions, feel free to reach out.
In this video, you’ll discover why glass prisms bend and separate light, demonstrating the principles of refraction.
This video illustrates how a prism operates to create rainbow colors, providing a visual understanding of light dispersion.