Chapter 1: Understanding Biological Scaling

As a child, the concept of pursuing Biology seemed amusing, but here I am, deeply engaged in it today. My interest has recently been ignited by Mathematical Biology, which has led me to explore various enigmatic aspects of life on our planet.

I have encountered numerous intriguing topics that have kept me awake at night, and one such concept is Kleiber’s Law. This principle reveals that when we compare the metabolic rates of different species relative to their body masses on a logarithmic scale, they align on a straight line with a slope of 3/4.

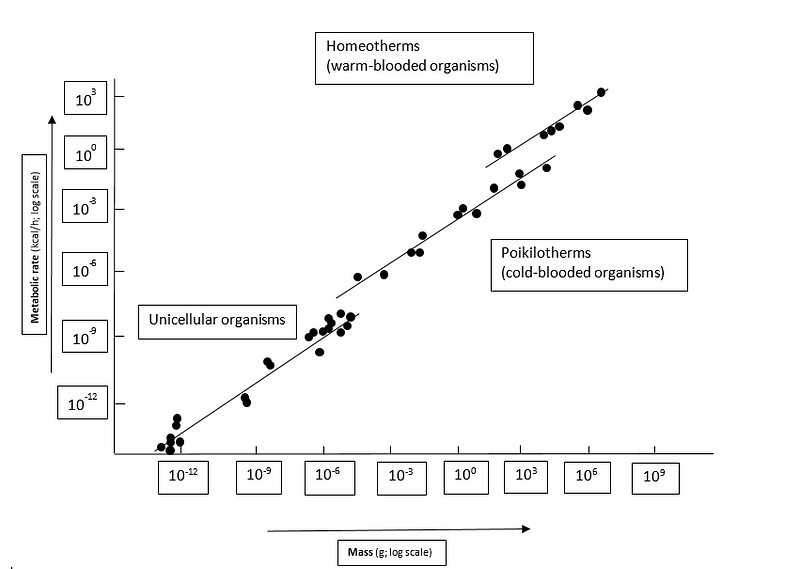
This relationship is astonishingly consistent, spanning from the tiniest bacterium to the largest whale—a difference of 20 orders of magnitude. To grasp the vastness of this scale, imagine multiplying 10 by itself twenty times to reach from the smallest bacterium to the largest whale.

When we examine metabolic rates, a clear hierarchy emerges: homeotherms have the highest rates, followed by poikilotherms, and then unicellular organisms. Surprisingly, while one might expect a linear relationship between metabolic rate and body size (as larger organisms generally have more cells), the reality is that metabolic rates decrease proportionately as body size increases. This implies that a mouse's metabolic rate is significantly higher relative to its body weight compared to that of a whale.

The reasoning behind this phenomenon is rooted in resource distribution. Small organisms can rely on simple diffusion for resource absorption, allowing for higher metabolic rates. For instance, bacteria thrive under these conditions. However, as organisms grow larger, diffusion alone cannot suffice. Instead, complex supply networks are necessary to meet their needs.

Insects utilize tracheoles for air transport, while mammals have intricate lung systems equipped with capillaries to facilitate gas exchange. Fish, too, possess gills designed for maximizing surface area for oxygen absorption. Even placentas utilize similar mechanisms to enhance nutrient transfer to developing embryos.

As the body size increases, the vascular network takes up more space, which can limit the area available for cells. If the number of cells doubles, the vascular network must expand even more than double to maintain efficiency. If it only doubles, the supply of nutrients and oxygen becomes inadequate, resulting in a decline in metabolic rate with increasing size.

Consequently, smaller animals exhibit quicker life processes, faster heart rates, and shorter lifespans. Interestingly, all mammals have an approximate limit of 1.5 billion heartbeats in their lifetime.

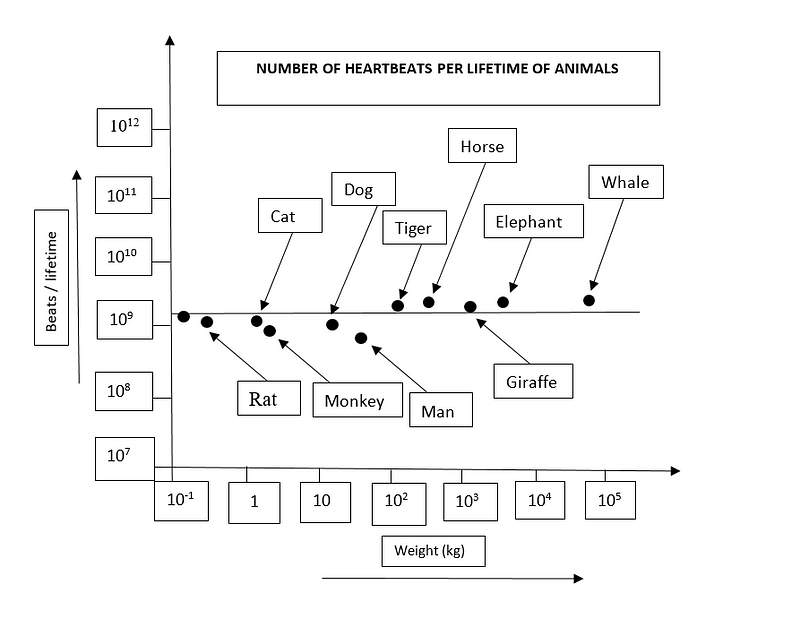
The limitations imposed by metabolic rates affect growth, as resources must be allocated to maintain existing cells rather than creating new ones.

Chapter 2: The Strength of Scaling

Scaling presents another intriguing aspect of biological life. The strength of any body part is proportional to its cross-sectional area, while overall body weight increases with volume. For instance, when length is doubled, area increases fourfold, but volume increases eightfold.

This geometric scaling means that as body size increases, relative strength diminishes. For example, if we imagined scaling a shrew to the size of an elephant, its slender legs would likely collapse under the increased weight. An ant, conversely, can carry objects many times its own weight due to its advantageous strength-to-weight ratio.

Elephants possess thick legs to support their massive bodies, a necessity for their size. Additionally, as body size increases, functions dependent on surface area, like heat transfer, become problematic. To combat this, elephants have evolved large ears that provide an extensive surface area for dissipating heat.

The implications of these scaling laws extend beyond biology to explain why certain entities, such as trees and humans, cannot grow indefinitely without structural adaptations to support their increased mass.

This leads to a fascinating discussion about the feasibility of gigantic creatures like Godzilla or the sandworms from "Dune," which would succumb to their own weight without sufficient physical support.

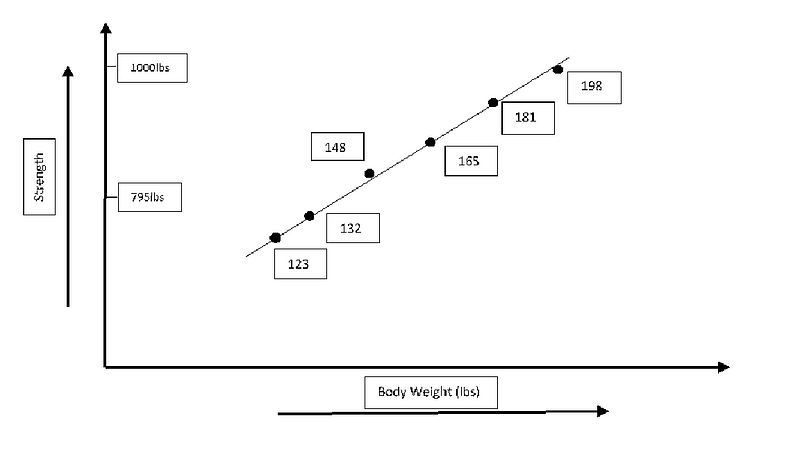
Practical demonstrations of scaling effects are seen in the realm of weightlifting. Research from the 1956 Olympic Games confirmed that strength scales at roughly two-thirds relative to body weight. This relationship was evident in the data collected on competitors, revealing a consistent pattern of strength relative to size.

Scaling laws also have significant implications in various fields. A study in 1962 concerning the administration of LSD to an Asiatic elephant highlighted the dangers of linear extrapolation. The research team calculated a dosage based on weight without considering metabolic differences between species, resulting in the tragic death of the elephant, Tusko. The researchers erroneously concluded that larger animals are proportionally more sensitive to drugs, failing to account for the fact that absorption occurs via surface area, not volume.

This miscalculation underscores the complexities of scaling in biological research. Given that most drug testing occurs in small mammals, applying those results to humans can lead to significant discrepancies.

The concept of scaling is not limited to biological organisms; it extends to societal structures and economies. Companies often experience rapid growth initially but tend to slow down as they mature, mirroring the patterns seen in biological scaling. A notable statistic is that half of all publicly traded companies fail within ten years.

Urban growth presents a dual scaling phenomenon; as cities expand, infrastructure demands per capita decrease, whereas socio-economic factors like wealth and innovation scale up. As cities grow, they tend to show systematic increases in various metrics, but this growth is ultimately constrained by finite resources.

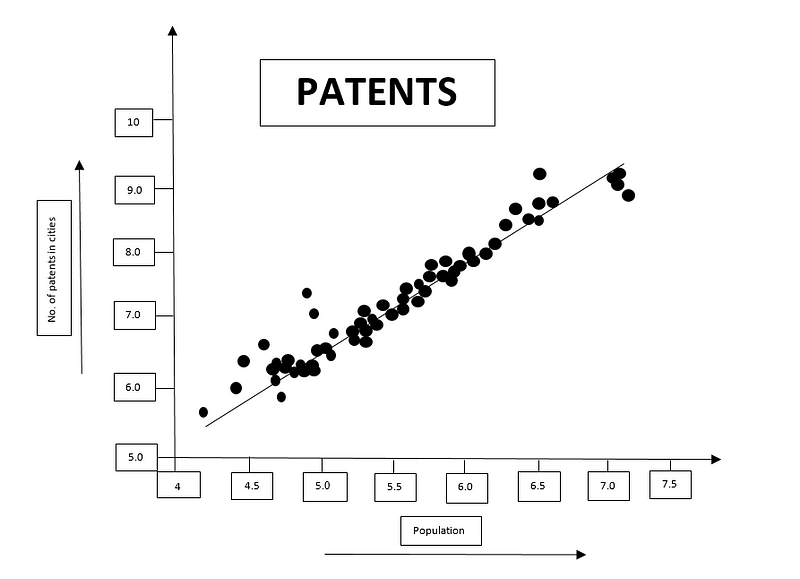
Ultimately, the principles of scaling reveal a universal language governing life, from the smallest cells to expansive cities, emphasizing the necessity for continuous innovation to avoid stagnation or collapse.

The first video titled "The Hidden Order of the Universe: Chaos Theory Explained" delves into the intricate mathematical laws that shape our understanding of life and nature, illustrating how these principles manifest across various scales.

The second video, "The World of Information | The Hidden Order in the Chaotic Digital Torrent," explores the parallels between information theory and the scaling laws observed in biological and social systems.