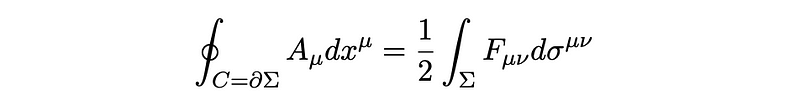Exploring Wilson Lines: A Geometric Perspective on Gauge Invariance
Written on
Chapter 1: The Necessity of Wilson Lines
As night falls, I find myself reflecting on the concept of Wilson lines. This discussion will align with insights drawn from Schwartz's work.
Section 1.1: Understanding Non-local Physics
Let’s delve into some fundamental questions regarding non-local physics. When fields possess a certain degree of gauge invariance, it becomes challenging to make comparisons between them at different locations. To illustrate this, consider a physical field denoted as phi. Given the symmetries present in our Lagrangian, we anticipate that this field exhibits some level of gauge invariance. Essentially, this means that at a specific point x in our field, we do not expect any variations in the physics when subjected to a transformation resembling
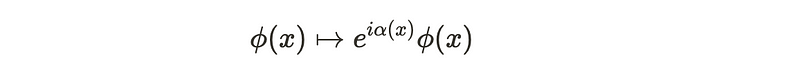
Now, if we assess the field at an alternate spatial point, the gauge field, represented by alpha in the previous expression, may not be local. Consequently, we can generally assert that
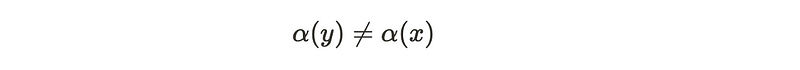
This raises philosophical questions; notably, it becomes impossible to ascertain whether the fields at various points are identical or distinct. For instance, consider two different points in our fields and evaluate their absolute magnitudes. Upon performing a gauge transformation on this absolute difference, the outcome may not remain unchanged.
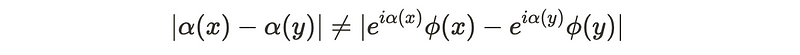
Section 1.2: Wilson Lines and Covariant Derivatives
Wilson lines provide a natural framework for constructing gauge invariant fields, enabling us to compare different points in spacetime meaningfully. Fields should remain invariant under a phase transformation ? (x) ? e^i?(x)? (x), yet this phase is not consistently the same across all points. Thus, gauge fields function as a connection, similar to concepts in general relativity, facilitating meaningful comparisons between fields at different locations. Schwartz elaborates on this concept further.
Revisiting Quantum Electrodynamics (QED), where fermions exhibit a U(1) gauge symmetry, we observe that under this transformation, the expression is given by
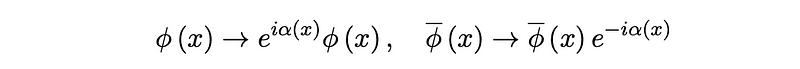
However, since ? (x) varies with x, our kinetic term ??/ does not retain its invariance. If we consider a derivative in the direction of a vector n, we find
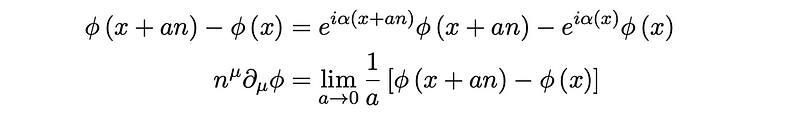
The gauge covariant derivative is defined to be the component that merely acquires a phase under this transformation, leading to
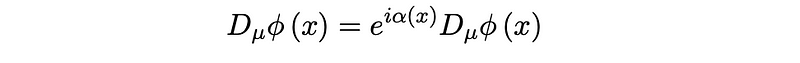
Defining Wilson Lines
We define a Wilson line (or parallel transporter) as a function represented as a line from x to y, such that its gauge transformation is expressed as ei?(y)W(y, x)e?i?(x). By convention, we establish that W(x, x) = 1. This leads to the conclusion that W(y, x) is purely a phase, allowing us to denote W(y, x) = ei?(y,x). We adopt the convention that W(x, y) = (W(y, x))^*.
With Wilson lines, we can also define the covariant derivative in a specified direction as follows:
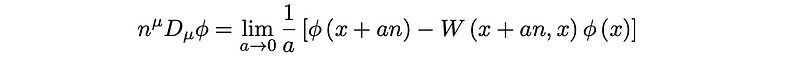
It can be verified that this expression is gauge invariant by transforming the contents within the brackets under U(1). The entire term adjusts simply by the phase e^(i?)(x+an). Since our vector n was arbitrary, it confirms that ?D?/ is indeed gauge invariant. From this Wilson line, we can further define the gauge field Aµ as the infinitesimal parameter in the exponential, expressed as
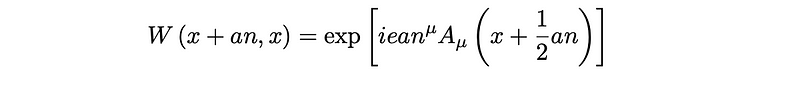
If we expand our exponential, considering we are operating in the limit where it is minimal, we derive the form of our covariant derivative as
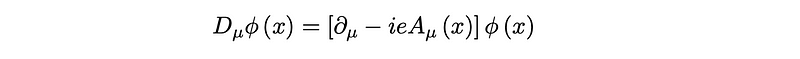
Through infinitesimal gauge transformations, we acquire the following identities:
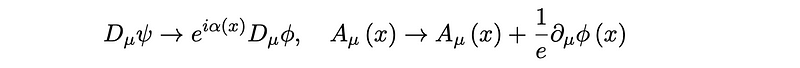
Chapter 2: Wilson Lines and Electromagnetism
Thus, since Dµ does not contribute anything additional to the transformation of a field that transforms as ? (x) ? e^(i?(x)) ? (x), we conclude that the composite operator D?Dµ adds no new elements. Particularly, this signifies that
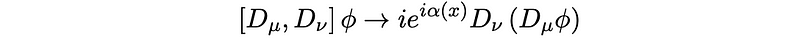
This directly corresponds to the electromagnetic field. Alternatively, we can create a ‘plaquette,’ which is formed as a square with vertices as follows:
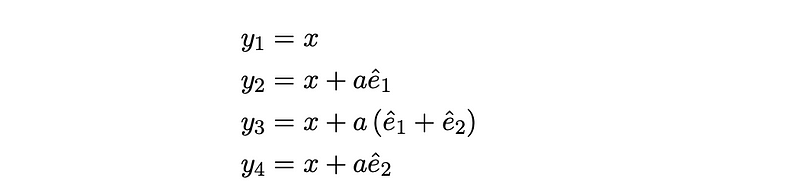
By expanding this around small a, and after canceling terms, we derive a form that resembles
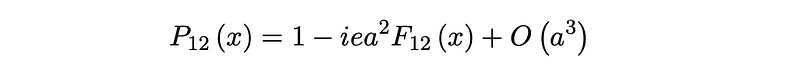
Consequently, we see the electromagnetic tensor emerging naturally during the construction of this square. Conversely, Wilson lines need not remain small, and with the field Aµ being continuous, we can define a curve C that acts as a Wilson line:
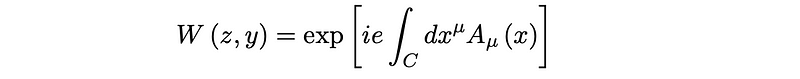
This curve forms a loop if y = z, with C = ?? where ? indicates the area enclosed. Applying Stokes’ theorem, we derive that