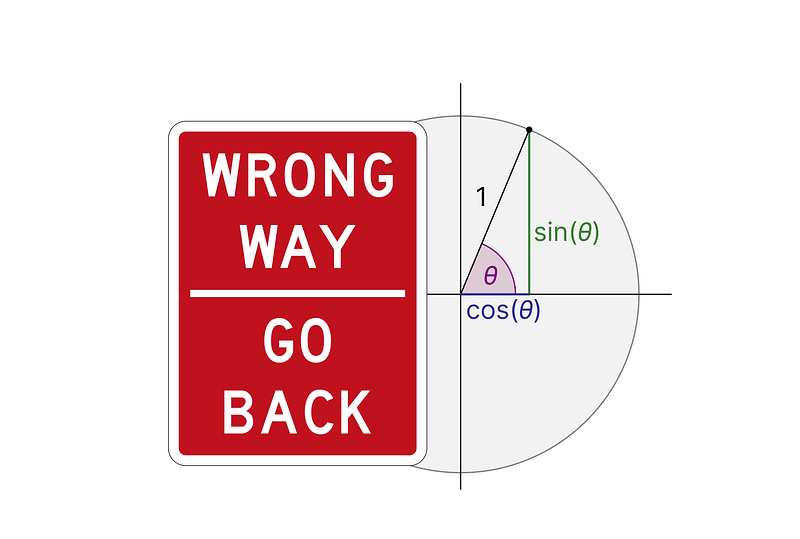
Rethinking Angle Definitions

Wildberger’s approach eliminates the need for calculus, transcendental numbers, and even irrational numbers—hence the term "rational trigonometry." He introduces new terms: quadrance and spread, replacing traditional notions of distance and angles, respectively.

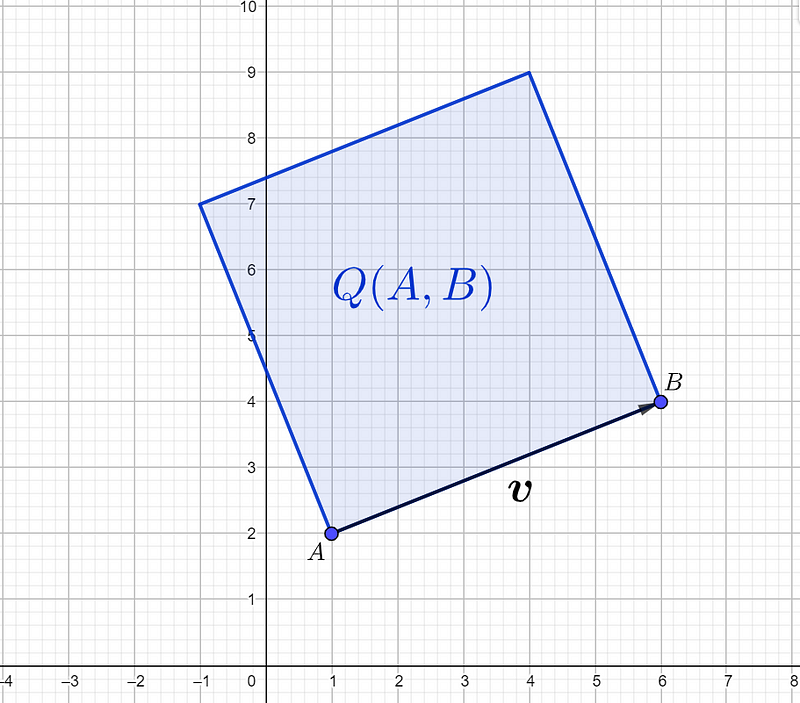
To define the quadrance of a vector v from point A to B, consider the area of the square formed by the side length AB.

The spread between two vectors, v and w, is determined by constructing a perpendicular segment and calculating the ratio of their quadrances.

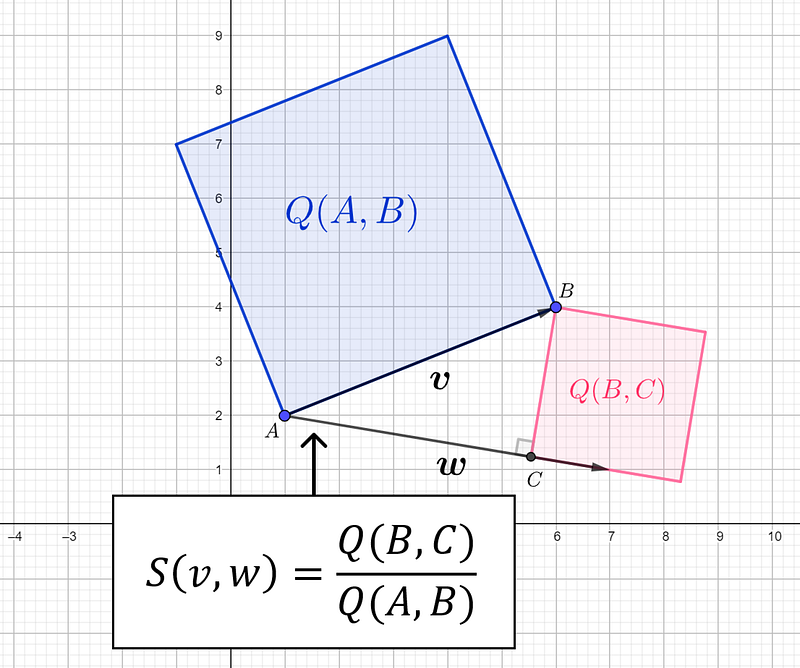
It's worth noting that quadrance is essentially the square of the distance between two points. In familiar trigonometric terms, spread can be represented as (sin θ)², where θ is the angle between the vectors. However, instead of relying on angles, the concept of spread is introduced as a replacement.

Calculating spread can be done precisely using Cartesian coordinates or vector forms, a luxury not afforded by most angles—except for certain convenient ones like 30°, 45°, and 60°.

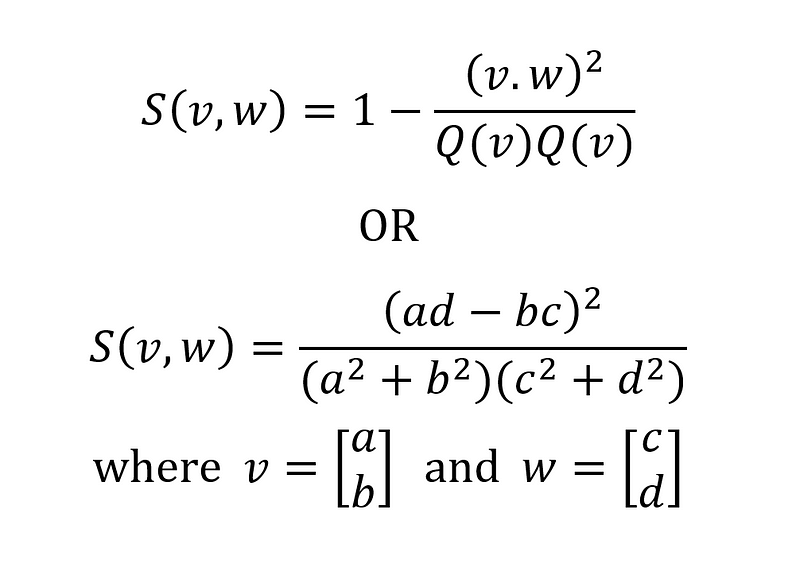
Example Spread Calculation

Let's look at a sample spread calculation.

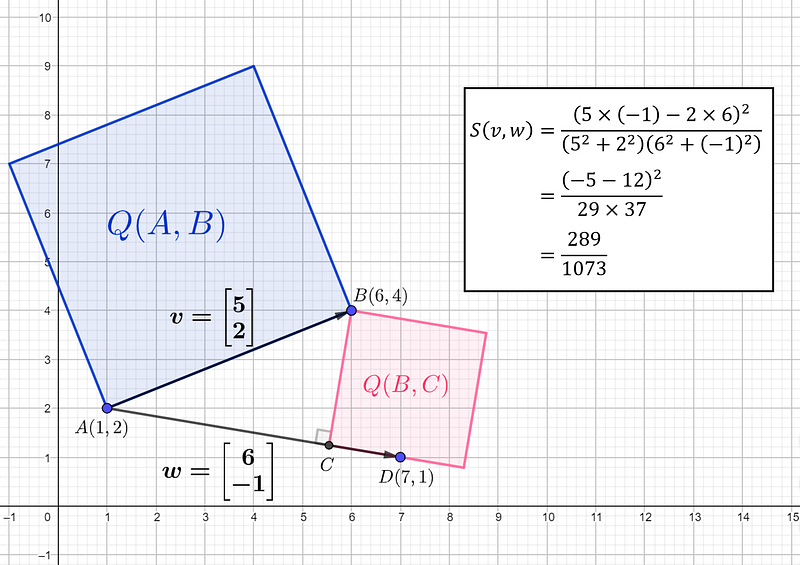
In rational trigonometry, the spread between two vectors will always yield rational results. This simplification allows for trigonometric calculations without needing to engage with calculus or irrational numbers.

If the spread calculation seems complex, consider attempting to find the angle between two vectors without using a calculator equipped with predefined trigonometric functions!

Laws of Rational Trigonometry

Many familiar geometric and trigonometric identities become more straightforward when expressed through quadrance and spread. For instance, the Pythagorean Theorem can be expressed simply as:

Q(a) + Q(b) = Q(c)

This simplicity is hard to beat!

There are also rational trigonometry equivalents for the sine and cosine rules.

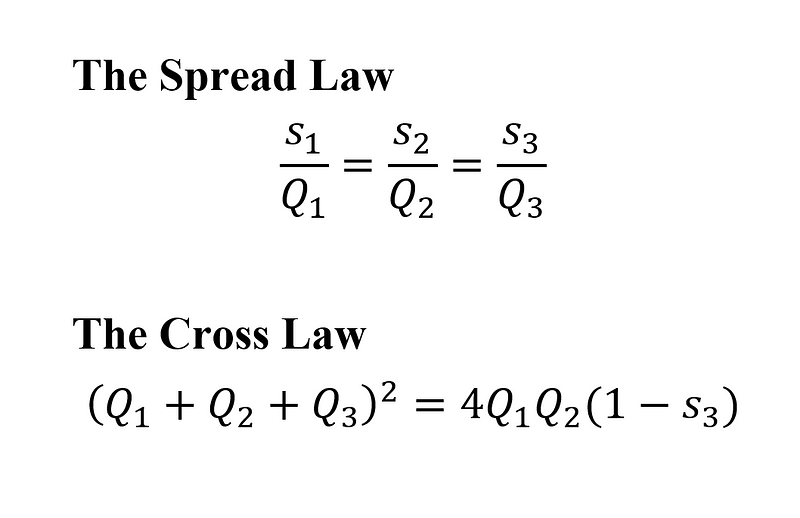
However, some familiar concepts take on a more complicated form in this new framework. The "triple spread formula," which parallels the triangle angle sum formula, can become cumbersome.

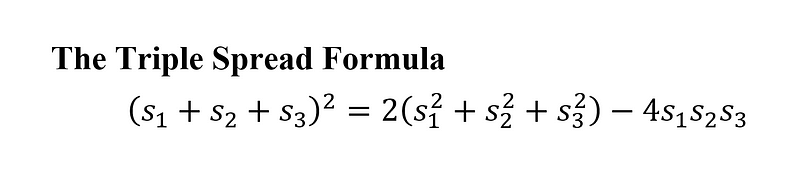
Moreover, instead of simply adding distances for parallel vectors, we must rely on the "triple quad formula":

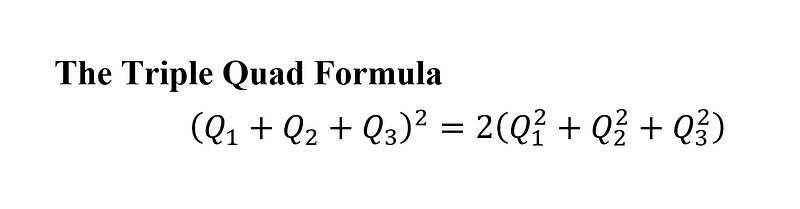
This shift from traditional distance to an area-based quadrance metric introduces a layer of complexity. For example, if you walk in the same direction at a consistent pace for 20 minutes, the distance covered is double that of 10 minutes. However, the quadrance increases by a factor of four, which can feel counterintuitive.

A 3D Application of Spread

Wildberger provides an interesting example in his 2007 paper. Imagine a plane inclined at a spread s to the horizontal. Instead of taking the steepest path, you walk at an angle r from this line of greatest slope.

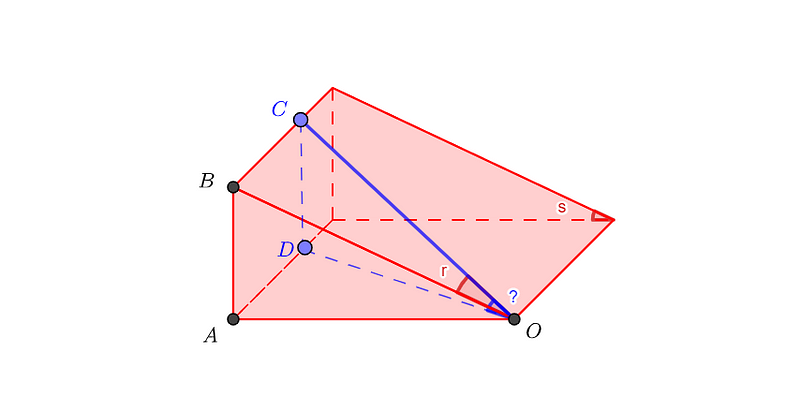
To find the spread between your path and the horizontal, we can set the segment OC's quadrance Q(O,C) to 1. From here, we can derive Q(B,C) = r due to the spread r between OB and OC.

Using the Pythagorean theorem on triangle CBO, we find:

Q(O,B) = Q(O,C) + Q(B,C)

Q(O,B) = 1 + r

Then, we can express the spread of s between OB and OA as:

s = Q(A,B) ÷ Q(O,B)

Q(A,B) = s × Q(O,B)

Thus, the desired spread can be represented as:

spread = Q(C,D) ÷ Q(O,C)

spread = Q(A,B) ÷ 1

spread = s × Q(O,B)

spread = s(1 + r)

Thoughts on Rational Trigonometry

Norman Wildberger is undoubtedly an exceptional mathematician. His rational trigonometry framework offers a logical alternative to conventional methods, focusing on squared distances and sine ratios.

I appreciate the ability to tackle trigonometric problems using solely rational numbers without delving into calculus or infinite series. As a high school math teacher, I sometimes encourage students to utilize squared distances for optimization problems as they are simpler to differentiate.

I also resonate with Wildberger's suggestion of introducing vectors before trigonometry. The transition from coordinate geometry to vector arithmetic feels seamless without the complication of angles.

In my opinion, while this framework makes some problems more straightforward and elegant, it complicates others. The example involving the 3D plane highlights relationships based on sine ratios; however, the loss of proportionality in distances strikes me as a fundamental issue.

It’s challenging to detach from my prior education to assess the merits and drawbacks of this new approach impartially. I find it more intuitive to understand angles as rotations—fractions of circles—rather than ratios of squares.

I find the argument for replacing the half-circle constant π (approximately 3.14159) with the full-circle constant τ (approximately 6.28318) more convincing, but that’s admittedly a minor conceptual shift.

The main hurdle for rational trigonometry may simply be the inertia of established educational practices. Perhaps in a century, we will reflect on our current "irrational trigonometry" with amusement.

Further Exploration of Rational Trigonometry

• "A Rational Approach to Trigonometry," N J Wildberger, Math Horizons (2007)
• Book: "DIVINE PROPORTIONS: Rational Trigonometry to Universal Geometry," N J Wildberger (2005)
• Insights into Mathematics (N J Wildberger’s YouTube Channel)
• Wikipedia article detailing critical responses to Rational Trigonometry

In this video, Wildberger discusses the complexities of traditional trigonometry and introduces his rational approach.

A beginner-friendly introduction to the basics of trigonometry, debunking the myth that it is a difficult subject.