Chapter 1: Understanding Light and Polarization

In classical electromagnetism, light behaves as a wave, generated by oscillating electric and magnetic fields that move perpendicularly to the direction of travel. This travel direction defines the polarization of the light wave. While polarization remains a crucial concept in quantum mechanics, its application to photons is less straightforward. A photon can exhibit two independent polarizations: vertical linear and horizontal linear. The limited number of independent polarizations is intricately linked to the symmetry inherent in our physical system. This chapter will delve into the principles of Lorentz invariance.

Chapter 1.1: The Lorentz Group and Its Significance

To grasp the concept of symmetry, we begin by examining the foundations of quantum field theory, where particles are represented by fields. These fields can be either single-valued and real or complex-valued, and for particles like electrons or photons, they may possess multiple components. Regardless of their nature, these fields cannot be arbitrarily defined; they must adhere to fundamental transformation properties aligned with symmetry principles. Specifically, our physical laws should remain unchanged when viewed from different perspectives.

In special relativity, these varying perspectives are encapsulated in the Poincaré group, which comprises two primary components. The first component is the symmetry related to translations, which is intuitive since we wouldn't expect observable physical quantities to vary merely due to a shift in our coordinate system. The second component involves symmetry concerning Lorentz transformations, which include standard rotations in space and Lorentz boosts that allow for transformations between reference frames moving at different velocities, all while keeping the speed of light constant.

Section 1.1.1: Representations of States in Quantum Theory

In light of these fundamental restrictions, we can draw meaningful conclusions about the nature of particles. Particles are represented as states within a larger mathematical framework known as Hilbert space, a subject of keen interest for physicists. To modify a state in Hilbert space, we apply a transformation operator. This transformation is represented by mappings.

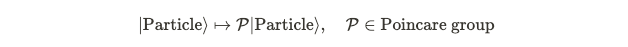
The notation ( mathcal{P} ) does not represent an actual element of the Poincaré group but rather a representation that interacts cohesively with the Hilbert space framework. Contractions of particle states typically yield observables, leading to the conclusion that these contractions should remain invariant under Poincaré transformations. For any two states, we have the following condition:

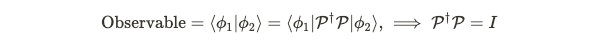
This condition is referred to as unitarity. Additionally, if the transformations preserve the integrity of the states, the representation is termed irreducible. With just a few symmetry assumptions, we conclude that particle state transformations are unitary and irreducible representations of the Poincaré group.

Chapter 2: Diverse Representations of the Poincaré Group

The Poincaré group can be illustrated through various objects that conform to its group structure, including scalars, vectors, and tensors. Each of these objects adheres to transformation laws — when coordinates are relabeled, the physical entities remain unchanged. For instance, consider the temperature in a room; it is a scalar field where each point is associated with a specific temperature. Under a coordinate relabeling, the field’s physical appearance remains constant. This is mathematically represented as:

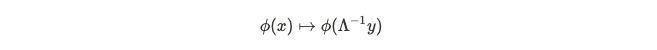
Here, the coordinate ( x ) signifies the coordinate system in our initial frame, while ( y ) denotes the second frame of reference following a coordinate relabeling. Transitioning between coordinate sets necessitates a Lorentz transformation, usually represented by the Greek letter Lambda.

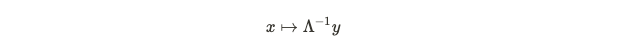
This mapping indicates that altering coordinate systems does not affect the field, as it represents a physical object. However, with vectors, the situation is a bit more complex. Vectors consist of components and are expressed as sums of basis vectors, which must transform correctly for vectors to represent physical entities that remain consistent under transformations. Consequently, a 4-component vector must transform according to the following rule:

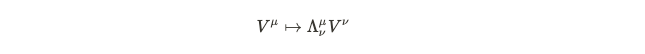
This principle extends to objects with multiple components, generally referred to as tensors. These tensors represent a Poincaré group representation, as they transform appropriately. However, they do not necessarily conform to unitary transformations. For example, if we consider a tensor, which can also be viewed as a matrix, taking its Hermitian conjugate will not satisfy the unitarity condition previously outlined. Thus, it becomes evident that finite-dimensional representations of the Poincaré group cannot be unitary; consequently, we must focus on infinite-dimensional representations. In 1939, Wigner classified the unitary irreducible representations of the Poincaré group, and I will discuss how to embed these representations into fields in a future article.

This video titled "Relativity #29 - The Lorentz and Poincaré Groups (Very briefly!)" offers a concise overview of the Lorentz and Poincaré groups, crucial for understanding the underlying symmetries in quantum theory.

Another insightful video, "The Poincaré Group - Symmetric Physics," elaborates on the significance of the Poincaré group in physics and its role in maintaining the symmetries of the universe.