Exploring the Distance Between Two Circles in Geometry
Written on
Chapter 1: Understanding the Problem
Have you ever looked at two circles and thought they resembled planets?
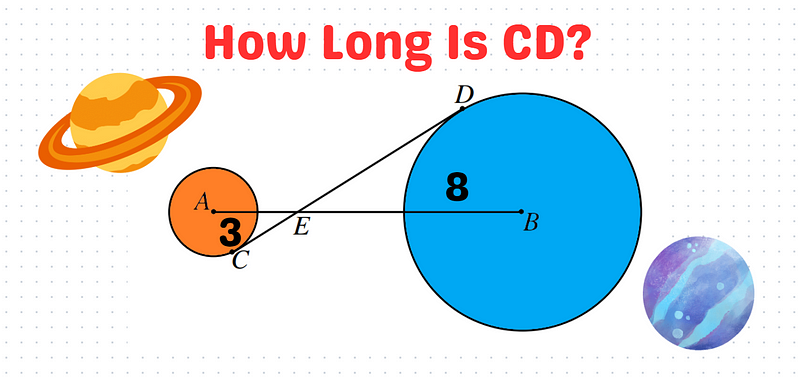
The orange circle has a radius of 3, while the blue circle's radius measures 8. The length of line segment AE is given as 5. Are you sharp enough to determine the length of segment CD?
I encourage you to pause for a moment, grab a pen and paper, and give it a try. Once you're ready, continue reading for the solution!
Section 1.1: Solution Steps
To start, we will connect points A to C and B to D.
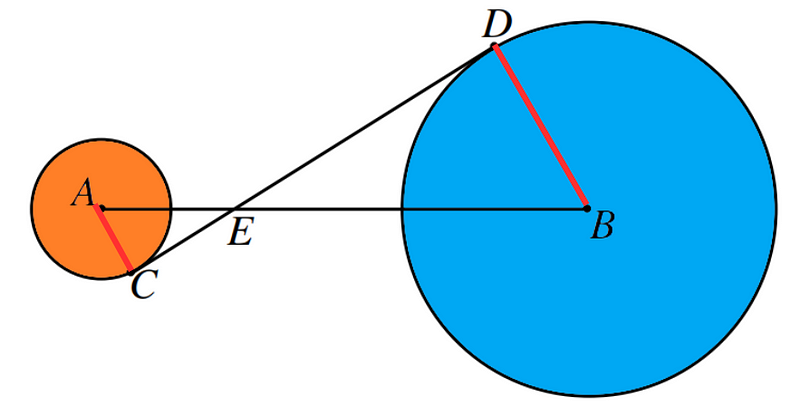
Here, we observe that the radii AC and BD are perpendicular to the line segment CD. We can utilize the Pythagorean Theorem in triangle ACE to determine the length of CE, which is part of line segment CD.
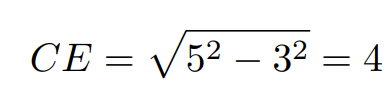
Now, take note of the two triangles formed: triangles ACE and BDE. All of their angles are congruent, indicating that the triangles are similar. (Do you know how to demonstrate this?)
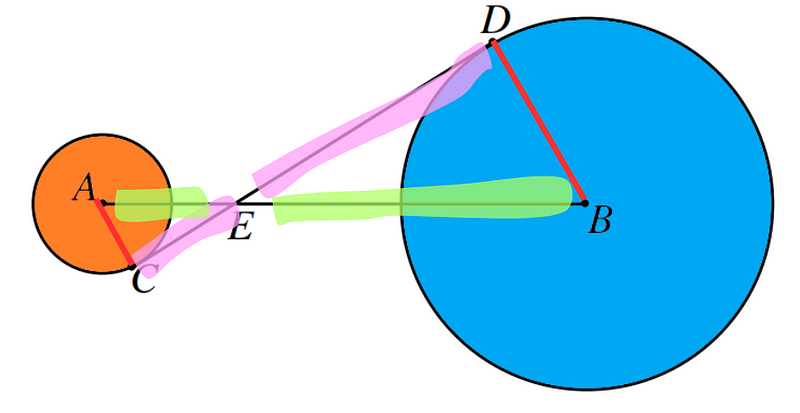
I have color-coded the sides of the triangles for clarity. Thanks to their similarity, we can establish the following ratio:
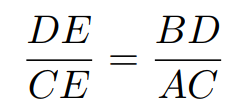
In this ratio, DE and CE are marked in purple, while BD and AC are in red. Our objective is to find DE. Given that CE equals 4, BD measures 8, and AC is 3, we can derive the following:
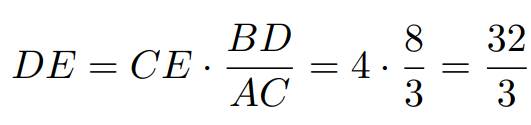
Here, BD represents the radius of the blue circle, and AC represents the radius of the orange circle. Now that we have determined the lengths for CE and DE, we can calculate the length of CD.

And there you have it—our answer!

This is quite fascinating, isn't it?
What was your thought process throughout this problem? I'd love to hear your comments below!
Chapter 2: Additional Resources
In the video titled "The Distance between Circles," you'll find a detailed exploration of calculating distances in geometry, which will enhance your understanding.
The second video, "Given Two Intersecting Circles, Find the Distance between Their Centers," provides insights on how to measure distances between intersecting circles, complementing our earlier discussion.
Thank you for reading! If you found this article helpful, please give it a clap. Your feedback is greatly appreciated!
