The Quest for an Ideal Quantum Computer: A Topological Perspective
Written on
Understanding Topology in Quantum Computing
In the realm of topology, a doughnut and a coffee cup can be considered equivalent due to their shared characteristic: the number of holes. This concept illustrates topology, which focuses on the properties of shapes that remain unchanged despite stretching or bending. For instance, altering a doughnut into a pretzel requires physically tearing it apart, demonstrating a change in topology.

Now, how does this relate to quantum computing? Think of a belt:
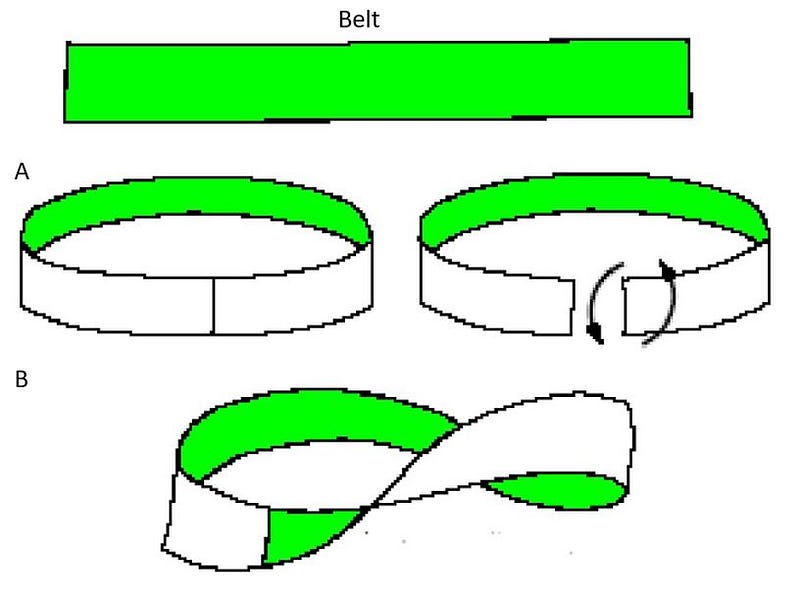
When you create a loop with a straight belt, it remains untwisted. However, if you twist it before looping, the twist becomes a permanent feature that cannot be removed without breaking the belt. This is analogous to how information can be preserved in a topological state, providing resilience against noise and accidental state collapse.
Topological Quantum Computing: Fundamentals
Topological quantum computing seeks to overcome decoherence by encoding information in a manner that external disturbances cannot affect. At the core of this technology are anyons—quasi-particles that exist uniquely in two dimensions.
What are Anyons?
Anyons are distinct from traditional bosons and fermions, possessing unique properties that allow them to retain a form of memory. In a three-dimensional space, particle exchanges revert to their original states, but in two dimensions, anyons retain information about their interactions.
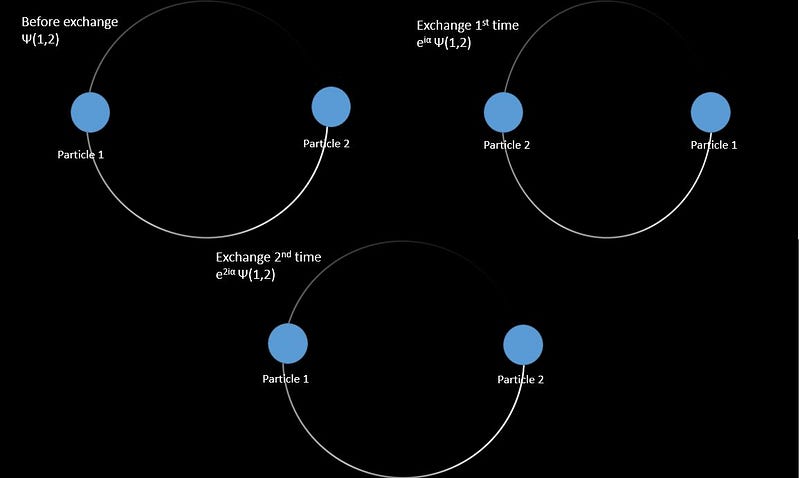
When anyons are exchanged in a two-dimensional plane, they do not revert to their initial state, creating a kind of memory based on their interactions. This characteristic makes them crucial for the development of topological quantum computing.
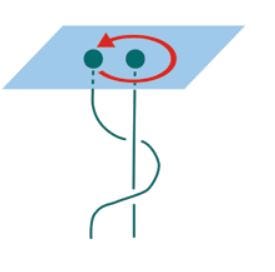
In this context, the act of manipulating anyons to encode information is referred to as "braiding." The ability to braid anyons creates a non-abelian structure, which is essential for the functioning of topological qubits.
Topological Qubits and Their Manipulation
A topological quantum system operates through three primary phases: Initialization, Gate Implementation, and Output Measurement.
- Initialization: In this phase, particle-antiparticle pairs are drawn from the vacuum to establish the initial states.
- Gate Implementation: The interaction and braiding of anyons occurs here, akin to applying gates in a quantum circuit. The specific braiding patterns represent various quantum gates.
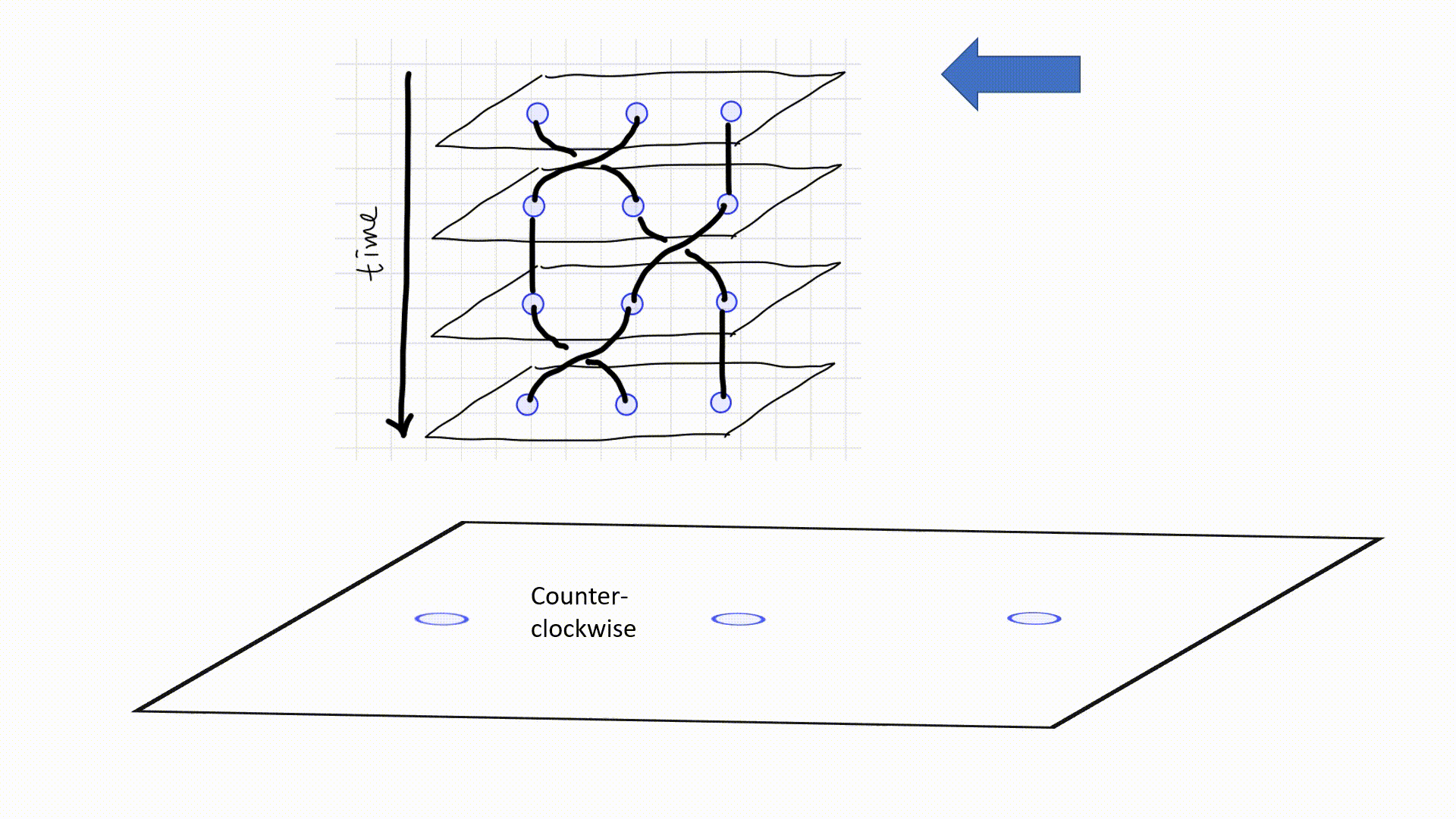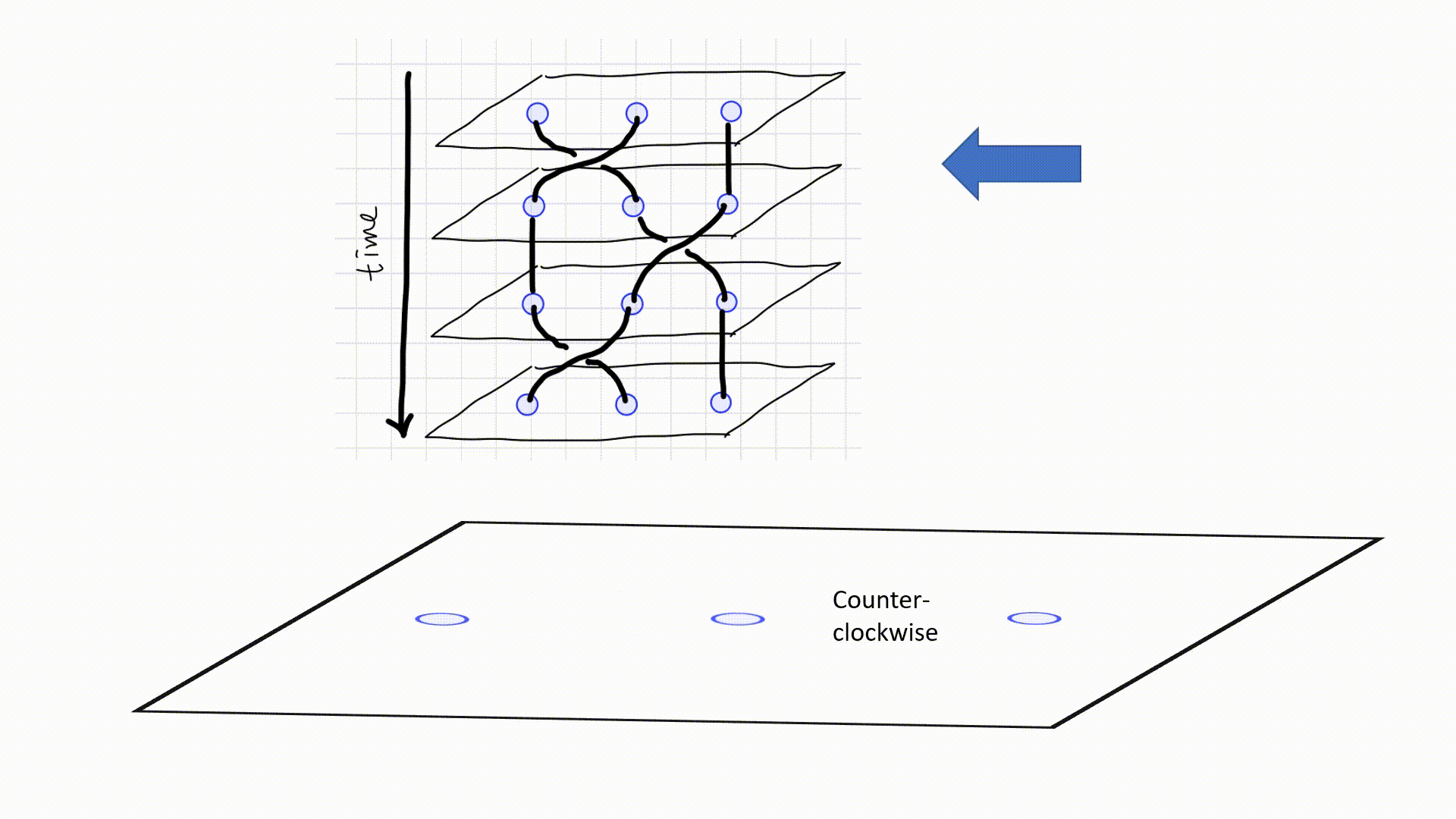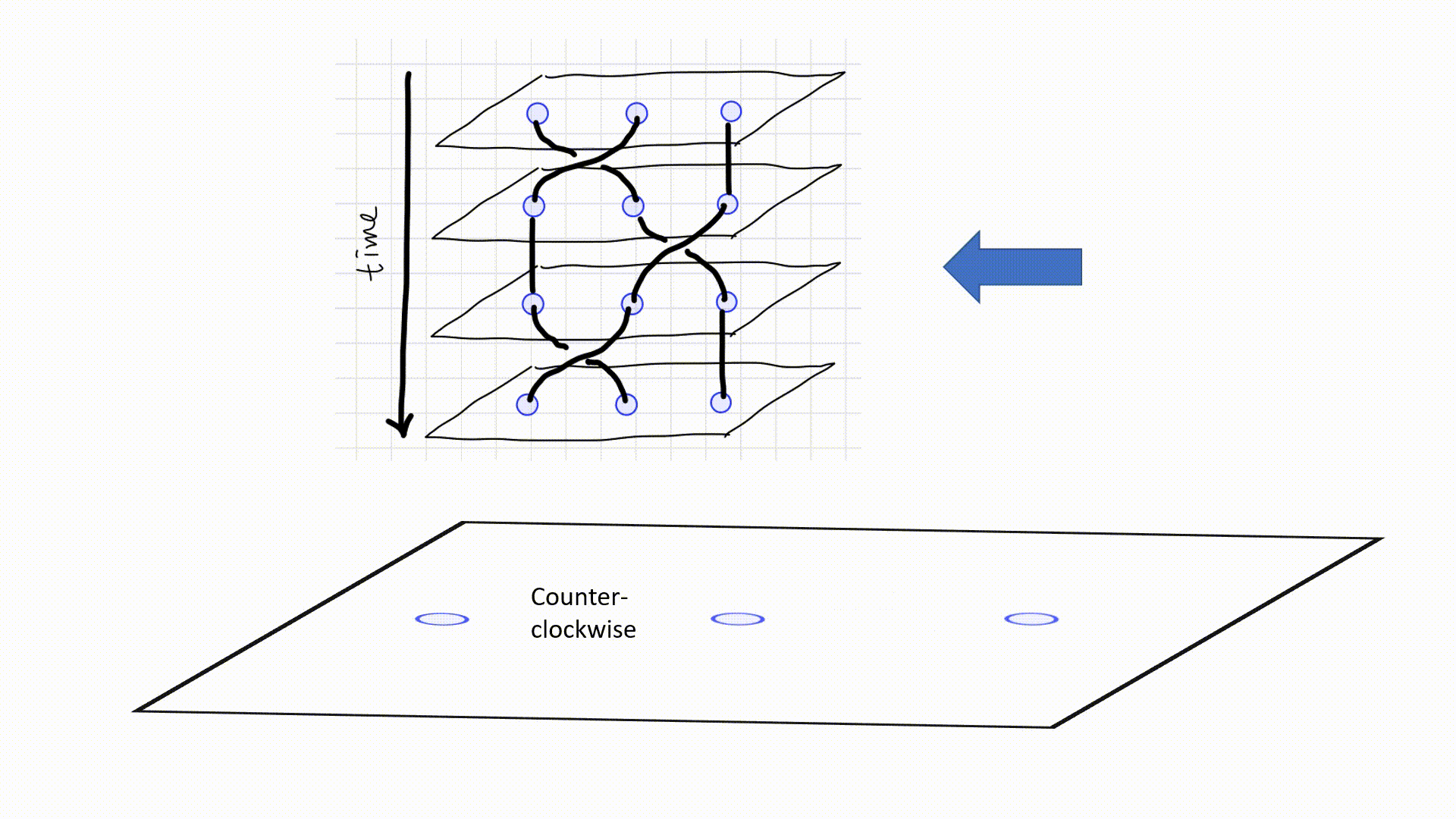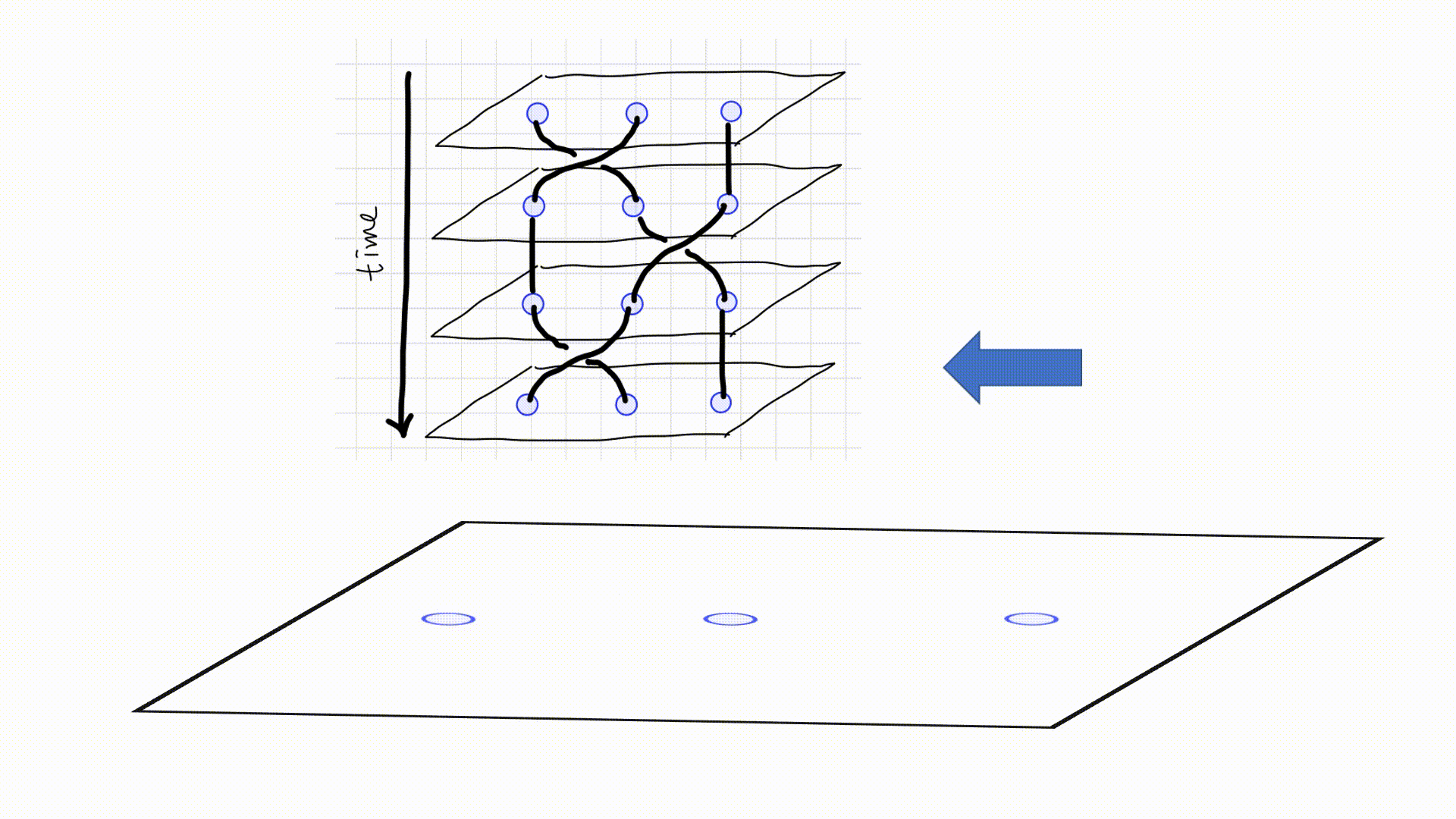
- Output Measurement: Finally, the states of the anyons are read to determine the outcomes of the quantum computations.
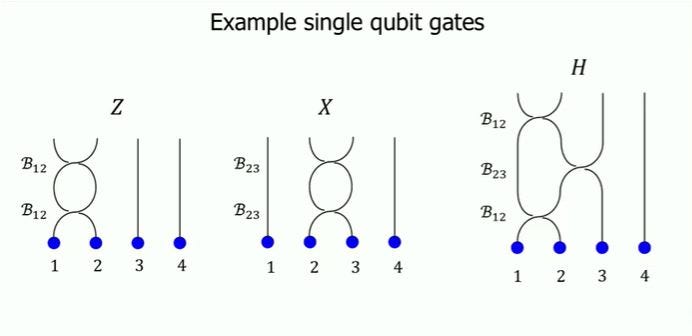
Advantages and Disadvantages of Topological Qubits
Advantages
- Resilience: Topological qubits are believed to be more robust due to their information encoding in topological properties, which are less susceptible to minor fluctuations.
- High Fidelity: Topological systems show a promise for achieving gate fidelity rates higher than conventional quantum systems, potentially reaching six or seven nines.
Disadvantages
- Lack of Prototypes: Currently, there are no working prototypes of topological qubits.
- Production Complexity: The creation of anyons requires advanced technology, making their development challenging.
- Limited Gate Accessibility: Due to the nature of discrete braiding operations, not all necessary gates for universal quantum computation can be achieved.
In conclusion, while the quest for perfect quantum computing continues, topological qubits present a fascinating avenue worth exploring.
Chapter 2: The Future of Quantum Computing
The first video titled "MIT Technology Review: The Race to a Million-Qubit Quantum Computer" offers insights into the ongoing competition in quantum computing technology.
The second video, "Building a Quantum Computer with Trapped Ions [QCT20/21, Seminar #09]," delves into the construction of quantum computers using trapped ions.
References
For more articles on quantum computing and machine learning, follow me on Medium, and connect with me on GitHub and LinkedIn.