Exploring the Two Envelopes Paradox: A Mathematical Dilemma
Written on
Chapter 1: The Envelopes Dilemma
Consider this thought experiment: You have two envelopes in front of you. You can choose one and observe the amount of money it contains. Let’s say you see $20.
The intriguing twist is that one envelope holds double the amount of the other. You are then given the opportunity to switch envelopes. Should you take that chance?

Photo by Liam Truong on Unsplash
At first glance, it seems switching shouldn’t make a difference. The situation appears symmetrical: there’s a 50% likelihood that the $20 represents the lesser amount and a 50% chance it’s the greater amount. Logically, it would seem that switching wouldn’t yield any additional benefit, suggesting that you wouldn’t gain anything from the switch.
However, let’s consider a different angle. What if I propose that switching could raise your expected winnings from $20 to $25? If the $20 is indeed the higher amount, switching would yield $10. Conversely, if it’s the lower amount, you would end up with $40.
Therefore, the expected value of your winnings can be calculated as follows:
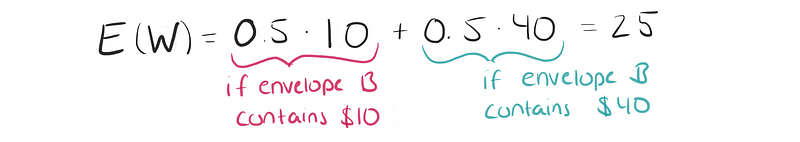
Given that you currently have $20 and switching offers an average return of $25, it seems reasonable to switch. This conclusion might startle you, just as it did me when I first encountered this puzzle. It’s even more perplexing than the well-known Monty Hall problem, which can be explained with relative ease.
However, upon deeper reflection, it becomes clear that this reasoning is flawed. If switching always led to an expected gain, one could argue for an infinite series of switches, leading to infinite profits. But beware—endless switching does not yield any actual benefits.
The calculation of the expected value is indeed incorrect. The critical question remains: why is that the case?
Section 1.1: A Simple Explanation
Let’s simplify the problem. Let’s say that in one envelope, you find an amount x, while the other contains 2x. If you initially select the envelope with x, switching would net you an additional x. Conversely, if you picked the envelope containing 2x, you would lose x by switching.
This leads us to an expected gain G of:
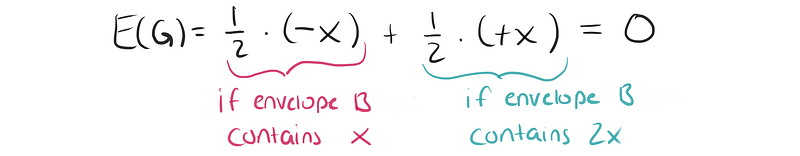
Thus, this reasoning seems coherent. So, where did our initial thought process go awry?
Subsection 1.1.1: Understanding Expected Values
The misunderstanding lies in how we define the random variable or the conditions we ignore. Just because we know one envelope contains twice as much as the other doesn’t imply a 50% chance that the second envelope contains twice the amount we observed in the first. It simply indicates that there is a 50% probability that the first envelope held 2x and a 50% chance it held x.
Let’s compute the expected amount of money in envelope A. There’s a 50% chance that it holds x and a 50% chance that it contains 2x. Therefore, the expected value in envelope A is:
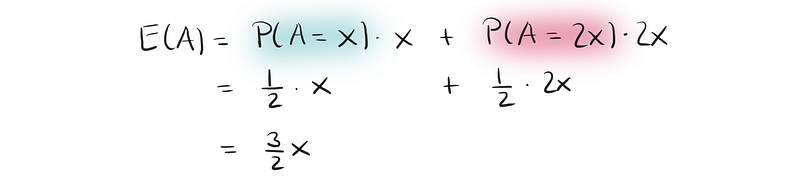
Before we open envelope A, the same logic applies to envelope B:
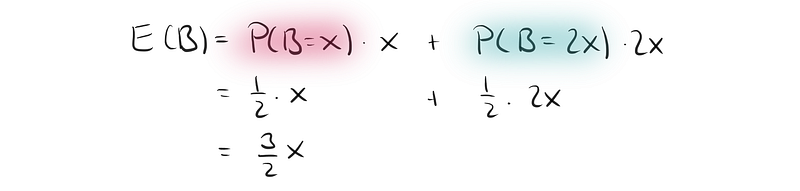
What happens once we open envelope A? Before opening it, the expected value in each envelope is 1.5x. The expected value of B remains unchanged; it’s just more complex to calculate post-opening. We now must consider conditional probabilities:
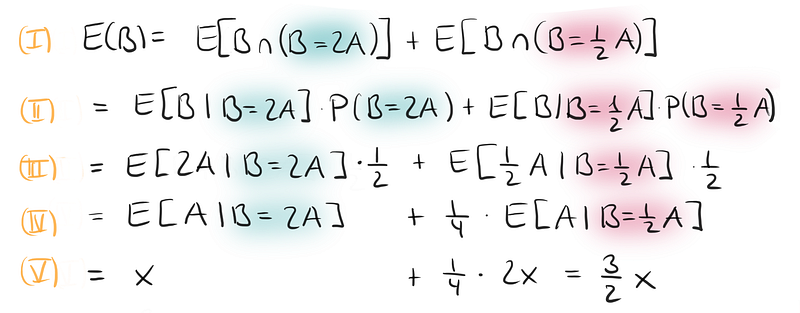
Despite the complexity, we arrive at the same conclusion: the expected value for envelope B is still 1.5x.
Section 1.2: Revisiting the Initial Miscalculations
Let’s return to our initial reasoning. While the previous explanation clarifies the correct answer, it doesn’t fully address why my first calculation of the expected value was incorrect. The crux lies in how we define our random variables. In my initial reasoning, I treated the amounts x and 2x as random variables, which they are not. They represent fixed (albeit unknown) values. Thus, there is no general 50% chance that the unopened envelope holds double the amount.
If we open the envelope with x, there is a 100% chance that the other envelope contains 2x. Conversely, if we open the envelope with 2x, there’s a 0% chance the other holds 2x.
The fixed amount x is not a random variable; rather, it’s a static value. That’s why we denote it with a lowercase letter. In contrast, the amounts in envelopes A and B are random variables, hence denoted with capital letters.
This distinction, although subtle, is crucial for grasping not only this paradox but also fundamental concepts in frequentist statistics!
Chapter 2: Origins of the Problem
Originally known as the necktie problem, this paradox involves two men who received neckties as Christmas gifts from their wives. They argued over whose necktie was cheaper and decided to consult their wives for the prices. They agreed that the man with the more expensive necktie would give it to the other.
Each man reasoned that, in the worst case, he would end up losing his necktie, but in a better scenario, he could gain the more expensive one, thus coming out ahead. Both men believed their reasoning favored them.
While it may be simpler to grasp the problem through the lens of money and envelopes, the rationale behind uncovering the flawed reasoning remains the same. There are numerous explanations to clarify this paradox. What’s your preferred approach?
This video titled "Should You Switch? NO!" explores the essence of the Two Envelopes Problem and the reasoning behind why switching may not yield a benefit.
In "One of the Weirdest Probability Paradoxes (The Two Envelopes Problem)," the complexities of this paradox are dissected, providing insight into its intricacies.