Chapter 1: Rethinking Electric Current

In the realm of physics, textbooks often present similar narratives. While they may vary slightly in their sequence or mathematical focus, many authors rarely question their chosen methods of explanation. This leads to a perception that there is a singular way to introduce concepts.

I challenge this notion. Exploring alternative methods of presentation is invigorating, albeit challenging, which may explain its rewarding nature. I want to clarify that I am not implying these alternative teaching methods surpass traditional ones; they simply offer different perspectives. Some may find these alternatives appealing, while others may not, but it's always beneficial to have options.

One of my primary frustrations when perusing physics textbooks is encountering assertions that lack experimental or theoretical support. Frequently, physical laws and definitions are presented as obvious truths, with little elaboration. Rarely do we see phrases like “it can be demonstrated that,” which essentially implies, “you may not grasp the reasoning, but trust me.” I, too, have resorted to this phrasing in my explanations, often to bypass formal proof, but I always aim to back up my conclusions with qualitative reasoning. Nonetheless, I find myself irritated when I must rely on it.

Photo by Nikola Johnny Mirkovic on Unsplash

Among the most perplexing definitions found in nearly every physics textbook is that of electric current, described simply as the flow of electric charges within a conductor. What is the origin of this definition? How can we confidently assert that a movement of charged particles constitutes current? Why do we express it as dq/dt, denoting the charge dq that crosses a surface over a time interval dt?

There are indeed valid reasons for this definition, but instead of recapping the historical context that led to this understanding—of which I must admit I am not entirely informed—I will attempt to introduce this concept through a fresh lens. This approach also highlights an essential topic, thermodynamics, which is often overlooked in discussions about electricity and magnetism, creating a misleading impression of their independence.

Let’s conduct a straightforward experiment: connect the terminals of a charged capacitor or a battery using a conductor. You will observe that the entire circuit heats up.

Thermodynamics informs us that the temperature rise correlates with the increase in the circuit's internal energy, represented by the equation:

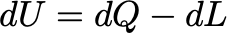
Here, dQ signifies the heat transferred to the circuit, which, in this scenario, is clearly dQ=0, as there are no external heat sources. Consequently, any increase in internal energy must be attributed to work performed by an external or internal force acting on the circuit. This work dL can be expressed as the product of a force F and a displacement dx: in this case, the only force we can envision is an electrical force, proportional to some charge q, and can be formulated as F=qE, where E is the electric field. The displacement dx refers to the movement of the charge. The negative sign conventionally indicates that the work is done on the system, but we can focus on its magnitude. Therefore, we can express this as:

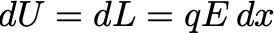
Power is defined as energy divided by time. Consequently, the power required to heat the conductor can be represented as:

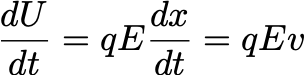
Here, v=dx/dt denotes the velocity of the charges. This implies that charges are indeed moving with velocity v within the conductor. We can also articulate this as:

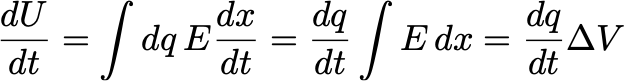
In this context, the line integral of E along the circuit represents the voltage difference ΔV. We can thus define the ratio dq/dt=I as the current, which is defined so that the power equals IΔV. This definition emerges naturally from our earlier discussion.

I find this alternative introduction of the current quite elegant, as it stems from fundamental principles. It also clarifies that the current flowing through a conductor is contingent upon the power involved. A portion of my students finds this perspective captivating; although they may have learned about current in high school, they often had no idea that first principles of thermodynamics could be applied to electrical circuits. This approach illuminates an important physical law, prompting them to reconsider its relevance beyond just the realms of gases and heat exchanges.

Chapter 2: Delving Deeper into Electric Currents

This video, titled "8.02x - Lect 9 - Electric Currents, Resistivity, Conductivity, Ohm's Law," provides an insightful overview of electric currents, resistivity, and the foundational principles of Ohm's Law.

The second video, titled "#physics #lectures at #ucla #electricity and #magnetism Series Lecture 7," further explores the intricacies of electricity and magnetism, enhancing our understanding of these critical topics in physics.